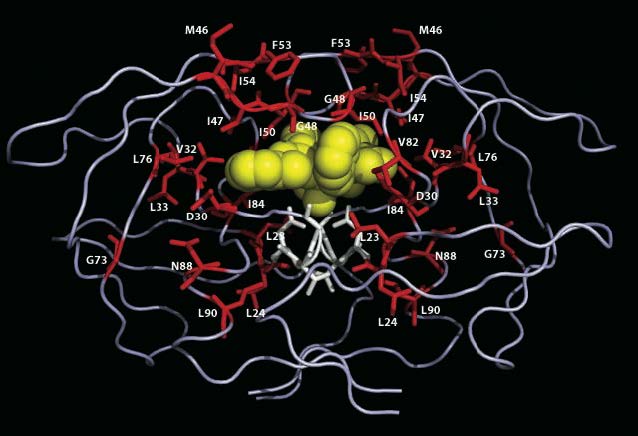
 Rendering of the HIV protease enzyme (from Stanford HIV drug resistance database) shows amino acids involved in conferring drug-resistance — a process which requires multiple mutations. Understanding the dynamics of natural selection as it facilitates or inhibits the intermediate stages of this exemplary evolutionary process is one of many problems where ideas from statistical physics may stimulate dramatic progress.
Rendering of the HIV protease enzyme (from Stanford HIV drug resistance database) shows amino acids involved in conferring drug-resistance — a process which requires multiple mutations. Understanding the dynamics of natural selection as it facilitates or inhibits the intermediate stages of this exemplary evolutionary process is one of many problems where ideas from statistical physics may stimulate dramatic progress.
Image credit: Dr. Robert W. Shafer (hivdb.stanford.edu).
The KITP’s new professorship, endowed by entrepreneur Gus Gurley in honor of his mother, is called the “Susan F. Gurley Chair in Theoretical Physics and Biology." Why “theoretical physics and biology”? The chair’s first incumbent, Boris Shraiman, addresses that question by first observing, “Biophysics is changing very rapidly."
“In the past,” he said, “biophysics was rather well defined. Physicists studied the physical properties of molecules and cells. For example, protein folding is clearly a physics problem. There are interactions, and you look for essentially a ground state for the fold that minimizes free energy.”
Another example of biophysics is the Hodgkin-Huxley model, according to Shraiman, “a beautiful combination of theory and experiment which established the mechanism for action potentials in axons,” the projecting parts of nerve cells that conduct impulses from the cells. “Still,” said Shraiman, “that work clearly deals with physical phenomena — electric currents and voltages — even though the phenomena are happening within cells.”
Second Wave Driven by Data
Hodgkin-Huxley exemplifies biophysics 50 years ago. “What is happening now,” said Shraiman, “is a second wave at the interface of physics and biology, driven by the overwhelming amount of data that now characterizes research in the life sciences.”
Sequencing techniques keep improving, and the improvements in turn foster a steady and almost exponential increase in data: genomes of different species enable interspecies comparisons; and genomes of different individuals enable intra-species comparisons.
“Amazing,” said Shraiman of the mounting mass of data, “and ‘amazing’ how little we learn from all this data.” He points to the some million differences in the genetic code for two sequenced individuals, DNA discoverer James Watson and Stanford bioengineer Steve Quake. “The great dream,” said Shraiman, “has been genetic medicine that will tell us whether a given individual will develop a given condition. But these genetic variants do not easily translate into phenotypes.”
Genetic variants determine the individual’s “genotype,” a blueprint that in turn determines the “phenotype” or the actual features and properties of the organism. As an architectural blueprint does not account for all of the interpretive and selected actions entailed in the dynamic process of actually constructing a building, so similarly is the relationship between genotypes and their phenotypic manifestations.
Said Shraiman, “When scientists manage to identify the alleles by gene variance that contribute to a given disease, what typically happens is that those alleles contribute very little. They explain a very small fraction of cases and leave most unexplained.” (An “allele” is one of a set of different forms for a given gene.)
“Alleles don’t contribute alone but in combinations,” said Shraiman, i.e., “interactions between many genetic variants determine the phenotype. We are only beginning to develop the tools to disentangle interactions and map the complex, multi-dimensional relation between the genotype and the phenotype.”
Need for Numbers
“Whenever you encounter complexity,” said Shraiman, “a good tool is being more quantitative. There is now consensus in the biology community that biology collectively has to become more quantitative. And, then, of course, comes the question, how does one accomplish that?”
One answer is through viruses. They afford a simple model with comparatively few genes and a model system with (again comparatively speaking) rapid evolutionary dynamics. “There is no better way of trying to uncover the causal connection [between genotype and phenotype through interacting genes],” said Shraiman, “than through access to this dynamical data.”
Richard Neher, KITP postdoctoral fellow working with Shraiman and recently named 2009 Harvey L. Karp Discovery Award recipient, has focused on the fact that to develop drug resistance a virus must generate not a single mutation, but a dozen mutations. Certain alleles (gene variants) will deliver an advantage in terms of drug resistance independent of what else is in the genome, but certain other alleles will only work well if in the company of “good friends,” so to speak. In other words, certain gene variants have to occur in the right combination in order to work.
Neher in his KITP talk “Sex, Viruses, and the Statistical Physics of Evolution” compared that “in-concert” operation of alleles to a “team” sport such as soccer where the quality of the team depends not only on the performance of individual players, but also on the way they work together.
“Once you have this complexity of interactions,” said Shraiman, “then the fundamental question is, ‘What is the effect of recombination?’” — i.e., sexual reproduction, which takes genes and reshuffles them. To recur to the sporting analogy, two very good teams can be reshuffled to yield a poor team.
“If you think, as physicists like to do, of a limit where a lot of recombination takes place, then it is intuitively clear, and can be shown mathematically, that these alleles start behaving independently in the sense that if you keep breaking up the teams, and still select the best, you are going to select genes that are beneficial, independent of the background (of any other gene). These are genes that work well in all circumstances (all-stars).”
Selection means that these genes are going to spread through the population, so there will be more of these variants that are individually better. But in doing that, some of the best genotypes (some of the best teams) may be lost because there could be pairs within these genotypes that work well together (better than anything), but selection on the basis of individual ability means loss of these genetic pairs.
This is the selfish gene regime, touted by Richard Dawkins, whereby genes are propagated on the basis of individual merit.
“But,” said Shraiman, “fitness is the property of the whole organism. You can think in terms of a capitalist society. How do you make a society work when all individuals only pursue their narrow self-interest? In population genetics, the answer is that the system works best if there is recombination, but not too much of it so that there isn’t too much self-interest.”
Shraiman explains the approach he and his collaborators at KITP have been developing. “We started with a population genetics problem,” he said, “and we redefined it as a statistical mechanics problem.”
From Thermo- to Population Dynamics
Statistical mechanics is the long-established theory of thermodynamic phenomena, describing states of matter in terms of thermal fluctuations and ensembles of particles. This theory basically provides a way of assigning probabilities to different configurations and then predicting the most likely outcomes of observations on these ensembles.
Of course, population dynamics is not governed by thermodynamics, but this statistical description of ensembles is still a useful way of thinking about the dynamics of populations. That creative and innovatively quantitative way of thinking suggests how the “Theoretical Physics” and the “Biology” of the Susan F. Gurley Chair go together.
“Once you start exploiting the mathematical analogy between these different descriptions” (of statistical mechanics and population genetics), said Shraiman, “it turns out to run surprisingly deep. We find essentially a phase transition between different regimes of selection: one regime of alleles selected on their own and another regime selected for the whole. This transition has a lot to do with glass transitions in spin glasses.”
(Particles have spin. In magnetic materials, the atomic forces cause neighboring spins always to align, thus producing a magnet. Glassy materials exhibit very disordered atomic interactions, and neighboring spins are confused as to which direction to align. Physicists call this phenomenon “frustration,” and in glassy materials it leads to the existence of many different states of equilibrium, in contrast to ordered materials in which a unique state of equilibrium is easily achieved.)
Quantitative modeling of population dynamics that reveals phase transitions akin to those in spin systems affords a first-rate example of how the plethora of detail that now characterizes the life sciences may, at least in part, reduce to overriding principles expressed in sets of equations. Of course, the life sciences are already informed by a great overarching theory — Darwinian evolution. And “theory” in science does not mean, as it does in common parlance, “hypothetical,” but “certain” with specified degrees of confidence ensuing from the scientific method of explaining, predicting, and verifying.
“In order to understand evolution,” said Shraiman, “scientists have to understand population genetics: how selection acts to control the spread of genes in the population."
“One of the early questions for us was the following: ‘Though we might expect great complexity of genetic interactions, is it possible that there is some dynamical evolutionary reason why actual living beings genetically would not be as complex as we could imagine?’"
“Let me try to argue that case. If (for whatever reasons) a population will propagate itself through sex and recombination, then there would be selection against interactions — selection against genetic complexity — and, instead, selection for alleles that would work well independently of what other alleles are doing. When we decipher an individual’s genome, it is not the variants that prove most useful and powerful in the population, but the units that have endured for millennia. Their endurance argues for selection for genetic simplicity.”
Luck Matters
“What really matters,” said Shraiman, “is existing a million years, and many genes have done just that, and within forms not imaginable at the time when the gene first appeared in the population. Thinking in terms of long-term survival means thinking in terms of units larger than single genes. A gene is a bunch of nucleotides, so already it's 500 individual little switches or base pairs. Maybe survival depends on a gene and its friend (another gene) or whole architectures of the genome such as its lifestyle understood in terms of mode of reproduction or sex.
“Ultimately, a gene survives a million years because it does, while millions of other variants haven’t. The survivor has to be not only good, but also lucky.”
Shraiman considers the opposite extreme: “Suppose the contribution of a given allele depends very strongly on what other alleles are doing. Then you ask what is the relation between the trait for the parents and the offspring? And you find there is none. Maybe that is the situation with intelligence — an ultimately complex trait that is not at all very heritable. That situation is called ‘transgressive segregation,’ and means that the distribution of offspring is much broader than the distribution for the parent.”
Seventy-five percent of Shraiman’s research now deals with questions raised by population genetics. The rest pertains to development or genetic unfolding morphologically. For instance, how does the fly progress from egg to larva to winged creature? His research, in other words, focuses on the two most obviously dynamical phenomena in biology — evolution and development. Why?
“Dynamics is where causal relationships become most easily observable,” said Shraiman.
- KITP Newsletter, Winter 2009
