Clarifications
During academic 2006-07 I spent a sabbatical year at Harvard. A freshman named Tim Hsieh, who was eager to learn quantum fieldtheory, was sent to me. He worked through my book and came to ask me questions once in a while. Sadly, I realized that my book was not perfectly clear and that freshmen, even at Harvard, occasionally have trouble understanding what I had written. Many of Tim's questions stemmed from gaps in his knowledge of quantum mechanics, which he had taught himself. I asked him to type up the answers I gave him on questions specifically related to my book. Here it is. I hope that other readers of the book would find these clarifying remarks helpful.
p. 14: To justify equation 14 with the coordinate transformation, the determinant of a matrix remains the same in all bases, which is why the easily found determinant of our diagonal matrix D is the same as the determinant of matrix A. Also, given that 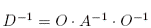 and the transformed
and the transformed 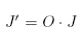 , the transformed
, the transformed 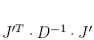 is the same as
is the same as 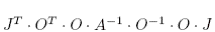 . Since O is orthogonal, that O’s disappear and we get the exponential on the right hand side of (14).
. Since O is orthogonal, that O’s disappear and we get the exponential on the right hand side of (14).
p. 15: To derive equation (16) (exercise I.2.2), differentiate both sides of (14) with respect to the different components of J to get the desired components of x in (17). Most of the resulting terms involve the exponential multiplied to a dot product involving J; these terms will disappear once we make J go to 0. The remaining terms are the Wick permutations, since these don’t have any dot products coupled to the exponential. For example, to get (18):
Differentiating the left side of (14) with respect to Ji, Jj, Jk, Jl and then taking the limit as J goes to 0, we get the numerator of (17). So now we must do the same to the right hand side of (14): Since we have divided by the denominator of (17), we no longer have to worry about the 2pi and determinant factor on the right hand side of (14). Differentiating with respect to Ji, we get
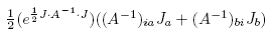
But A, and hence A-1, is symmetric, so we get
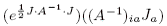
Differentiating with respect to Jj, we get
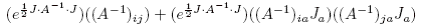 .
.
Now we differentiate with respect to Jk and then Jl. Most of the resulting terms involve the exponential multiplied to a dot product involving J; these terms will disappear once we make J go to 0. The only remaining terms, after we make J go to 0, are those three on the right hand side of (18).
p. 23: The signs of all 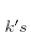 in the exponents do not matter since we are integrating from negative to positive infinity for all the integrals on the page.
in the exponents do not matter since we are integrating from negative to positive infinity for all the integrals on the page.
p. 23: We distinguish the two cases 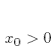 and
and 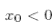 because we have to make sure that the exponential
because we have to make sure that the exponential 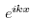 doesn’t blow up when we do the contour integral- that’s why we associate one path with
doesn’t blow up when we do the contour integral- that’s why we associate one path with 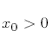 and the other with
and the other with 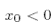 .
.
p. 23: The 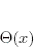 function is the Heaviside step function:
function is the Heaviside step function:
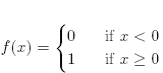
p. 27: In the line before “Connected vs. Disconnected”, it helps to know that momentum is the inverse of displacement when Planck’s constant is set to 1.
p. 112: To understand why the commutation relation implies that the K generators transform as 3-vectors, please see Appendix B and consider the following example: acting with a rotation about J1, for instance, we get
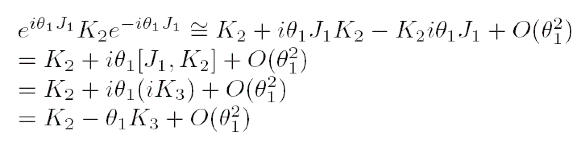
which is how the second component of a 3-vector transforms for small theta.
p. 127: Regarding Feynman rule #6, the -1 arises from a vacuum fluctuation of the fermion field, which, as we saw earlier, carries a negative vacuum energy.
p. 179: For the claim “The coefficient of the first term is the electric charge observed…”, please see the bottom paragraph of p. 178.
p. 219: For the second calculation,

where summing over nu and mu justifies the first step; the negative sign comes from switching the order of the two differentials and we divide by 2 because we have counted each pair twice. We exchange indices in the second term of the second step.
p. 223: The second exponent at the bottom of the page is conjugated because the exponent on the right side, which involves the whole clockwise path, requires a reversal of direction for the P2 path.

p. 231: For equation 19, we deal with U(N) in this case because in SU(N), there is a traceless condition which makes Eq. 19 much more complicated (if Ta is traceless, then we need to subtract terms in the form of products of Kronecker deltas).
p. 246: For the limit expression before equation (3), we are using Gauss’ theorem over all space (infinite surface integral, taking P (the radius of the sphere) going to infinity).
p. 371: To elaborate the last line before “Renormalization Group Flow”, the second inequality implies that
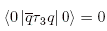
which implies
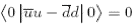
which implies that isospin symmetry isn’t broken. Similarly,
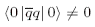
implies that
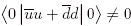
which, along with the equation two lines above, implies that neither composite of quarks is nonzero, so chiral symmetry is broken.
p. 391: As an example, (1,2,-1/2) and (1,1,-1) represent leptons since the 1 signifies that they do not take part in the strong interaction.
p. 397: By angular momentum conservation alone, the electron could decay into a neutrino and a photon, but charge conservation ensures that this does not happen.
p. 393: I think that in (11), nu and e should be interchanged, and the corresponding changes must be made to p. 402 (i.e., five lines below (12), it should be “electrically neutral fifth component” along with corresponding changes in the subsequent equations).
p. 410: To clarify, the tau matrices (and combinations of tau matrices) act on the group (spinor) representations of the epsilons; for instance,
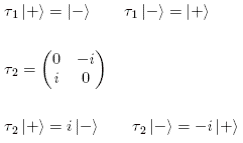
p. 412: To clarify, the 16+ are the observed particles (the 16-, such as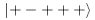 , are not observed).
, are not observed).
